Integration in Excel

1 minute read

In this post, I will show you how to integrate the Portfolio Optimizer Web API in Excel.

As a working example, I will display the assets weights $(w_1, w_2)$ of randomly generated long-only portfolios of 2 assets in a 2D Excel scatter plot.

The set of points spanned in $\mathbb{R}^2$ by these assets weights should theoretically be:

Either the probability simplex of $\mathbb{R}^2$, in case a full investment budget constraint $w_1 + w_2 = 1$ is imposed
Or the (full dimensional unit) simplex of $\mathbb{R}^2$, in case a partial investment budget constraint $w_1 + w_2 \leqslant 1$ is imposed

Let’s verify this!

Note: A fully functional Excel workbook corresponding to this post is available here.

Integration of the Portfolio Optimizer API in Excel

Working with Web APIs is not one of the strong points of Excel, but hopefully, some third party libraries are offering Web API communication capabilities.

One of the most well-known such libraries is VBA-Web, by Tim Hall.

I will rely on the helpers from this library to integrate the Portfolio Optimizer API in the example below.

Example of integration: displaying the assets weights of random portfolios

Portfolio Optimizer provides an API endpoint to generate random portfolios, that is, portfolios made of random assets weights: /v1/portfolio/construction/random.

Using VBA-Web, the integration of this Random Portfolio API endpoint can be done through the following skeleton VBA macro:

This skeleton VBA macro could then be improved to:

Read its inputs dynamically
Write the received random assets weights
Be automatically triggered upon a change of one of its inputs, or upon a click on a form button

This would give an Excel sheet similar to:

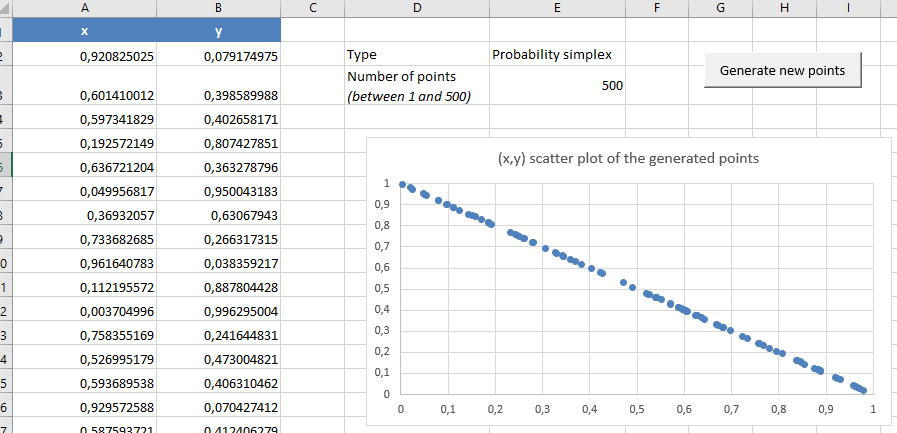
With it, it would be possible to verify that the set of points spanned in $\mathbb{R}^2$ by the assets weights of the random portfolios is:

The line joining the two points $(0,1)$ and $(1,0)$, in case a full investment budget constraint is imposed
The triangle joining the three points $(0,0)$, $(0,1)$ and $(1,0)$, as well as its interior, in case a partial investment budget constraint is imposed

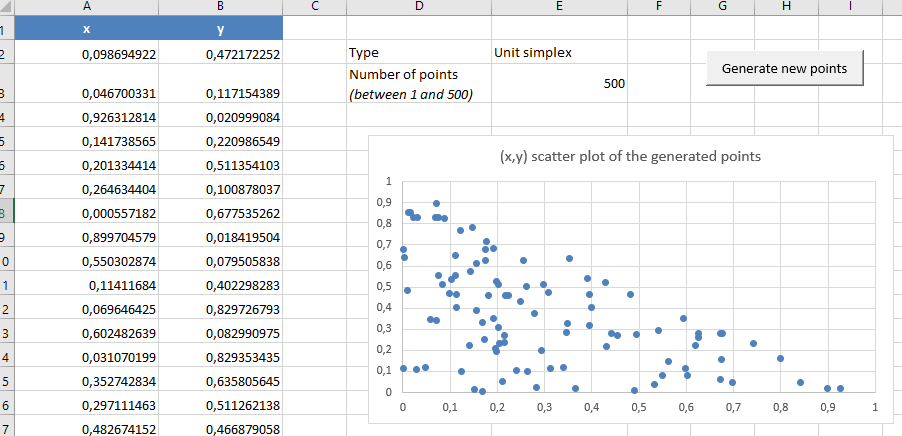
So, all good, the theory has been verified in practice!