Covariance Matrix Forecasting: Iterated Exponentially Weighted Moving Average Model

In the previous post of this series on covariance matrix forecasting, I reviewed both the simple and the exponentially weighted moving average covariance matrix forecasting models, which are straightforward extensions of their respective univariate volatility forecasting models to a multivariate setting.

With these reference models established, we can now delve into more sophisticated approaches for forecasting covariance matrices¹.

In this blog post, I will describe the iterated exponentially weighted moving average (IEWMA) model that has recently² been introduced in Johansson et al.³ and I will illustrate its empirical performances in the context of monthly covariance matrix forecasting for a multi-asset class ETF portfolio.

Mathematical preliminaries

Covariance matrix modelling and covariance proxies (reminders)

This sub-section contains reminders from a previous blog post.

Let $n$ be the number of assets in a universe of assets and $r_t \in \mathbb{R}^n$ be the vector of the (logarithmic) return of these assets over a time period $t$ (a day, a week, a month..), over which the (conditional) mean return vector $\mu_t \in \mathbb{R}^n$ of these assets is supposed to be null.

Then:

• $r_t$ can be expressed as⁴ $r_t = \epsilon_t$, with $\epsilon_t \in \mathbb{R}^n$ an unpredictable error term, often referred to as a vector of “shocks” or as a vector of “random disturbances”⁴, over the time period $t$

• The asset (conditional) covariance matrix $\Sigma_t \in \mathcal{M}(\mathbb{R}^{n \times n})$ is defined as $\Sigma_t = \mathbb{E} \left[ r_t r_t {}^t \right]$

  From this definition, the outer product of the asset returns $ r_t r_t {}^t $ is a covariance estimate - or covariance proxy⁵ - for the asset returns covariance matrix over the considered time period $t$.

• The asset (conditional) correlation matrix $C_t \in \mathcal{M}(\mathbb{R}^{n \times n})$ is defined as $ C_t = V_t^{-1} \Sigma_t V_t^{-1} $, where $V_t \in \mathcal{M}(\mathbb{R}^{n \times n})$ is the diagonal matrix of the asset (conditional) standard deviations.

Correlation matrix modelling

In order to clarify the relation between conditional correlations and conditional variances⁶, Engle⁶ proposes to write the [asset] returns as the conditional standard deviation times the standardized disturbance⁶, that is

\[r_{i,t} = \epsilon_{i,t} = \sigma_{i,t} \varepsilon_{i,t}, i=1..n\]

, with:

• $\sigma_{i,t} = \sqrt{ \mathbb{E} \left[ r_{i,t}^2 \right] } $
• $\varepsilon_{i,t}$ a standardized disturbance that has mean zero and variance one⁶

This way, the conditional correlation [between asset $i$ and asset $j$ becomes equal to] the conditional covariance between the standardized disturbances [$\varepsilon_{i,t}$ and $\varepsilon_{j,t}$]⁶

\[\rho_{ij,t} = \frac{\mathbb{E} \left[ r_{i,t} r_{j,t} \right]}{\sqrt{ \mathbb{E} \left[ r_{i,t}^2 \right] \mathbb{E} \left[ r_{j,t}^2 \right] }} = \mathbb{E} \left[ \varepsilon_{i,t} \varepsilon_{j,t} \right]\]

The iterated exponentially weighted moving average covariance matrix forecasting model

The IEWMA covariance matrix forecasting model³ is a two-step model that:

1. Uses an EWMA volatility forecasting model with squared asset returns as variance proxies in order to forecast asset volatilities
2. Uses an EWMA correlation matrix forecasting model with outer products of (EWMA-)volatility-standardized asset returns as covariance matrix proxies in order to forecast asset correlations

Johansson et al.³ highlights that the IEWMA model was originally⁷ proposed in Engle⁶ as an efficient alternative to the DCC-GARCH⁶ predictor, although he did not refer to it as IEWMA⁶.

In other words, the IEWMA covariance matrix forecasting model bridges the gap between the simple EWMA model and the more complex DCC-GARCH model.

Forecasting formulas

Let be:

• $n$ be the number of assets in a universe of assets
• $r_t r_t {}^t$, $t=1..T$ the outer products of the asset returns over each of $T$ past periods
• A decay factor $\lambda_{vol} \in [0, 1]$
• A decay factor $\lambda_{cor} \in [0, 1]$

Next period’s asset returns covariance/correlation matrix

The IEWMA covariance matrix forecasting model estimates the next period’s asset returns covariance matrix $\hat{\Sigma}_{T+1}$ and correlation matrix $\hat{C}_{T+1}$ as follows³:

• For each asset $i=1..n$ in the universe of assets
  • Forecast the asset one-period-ahead variances $\hat{\sigma}^2_{i,2}$, …, $\hat{\sigma}^2_{i,T+1}$ using an EWMA volatility forecasting model with decay factor $\lambda_{vol}$ and squared asset returns $r_{i,t}^2$, $t=1..T$, as variance proxies

  • Compute the volatility-standardized asset returns $\tilde{r}_{i,2},…,\tilde{r}_{i,T}$ defined as the asset returns standardized by their one-period-ahead EWMA volatility forecasts

    \[\tilde{r}_{i,t} = \frac{r_{i,t}}{\hat{\sigma}_{i,t}}, t = 2..T\]

• Compute the diagonal matrix of the assets next period’s forecasted volatilities $V_{T+1}$

  \[V_{T+1} = \begin{pmatrix} \hat{\sigma}_{1,T+1} & 0 & ... & 0 \\ 0 & \hat{\sigma}_{2,T+1} & ... & 0 \\ ... & ... & ... & ... \\ 0 & 0 & ... & \hat{\sigma}_{n,T+1} \end{pmatrix}\]
• Forecast the next period’s asset returns correlation matrix $\hat{C}_{T+1}$ using an EWMA covariance matrix forecasting model with decay factor $\lambda_{cor}$ and outer products of volatility-standardized asset returns $\tilde{r_t} \tilde{r_t} {}^t$, $t=2..T$, as covariance matrix proxies

• Compute the next period’s forecasted asset returns covariance matrix $\hat{\Sigma}_{T+1}$

  \[\hat{\Sigma}_{T+1} = V_{T+1} \hat{C}_{T+1} V_{T+1}\]

Next $h$-period’s ahead asset returns covariance/correlation matrix

The IEWMA covariance matrix forecasting model estimates the next $h$-period’s ahead asset returns covariance matrix $\hat{\Sigma}_{T+h}$ and correlation matrix $\hat{C}_{T+h}$, $h \geq 2$, by the next period’s asset returns covariance matrix $\hat{\Sigma}_{T+1}$ and correlation matrix $\hat{C}_{T+1}$.

Indeed, due to the properties of the EWMA volatility and covariance matrix forecasting models⁸, we have:

• $V_{T+h} = V_{T+1}$, $h \geq 2$
• $\hat{C}_{T+h} = \hat{C}_{T+1}$, $h \geq 2$

So that $\hat{\Sigma}_{T+h} = \hat{\Sigma}_{T+1}$, $h \geq 2$.

Averaged asset returns covariance/correlation matrix over the next $h$ periods

The IEWMA covariance matrix forecasting model estimates the averaged⁹ asset returns covariance matrix $\hat{\Sigma}_{T+1:T+h}$ and correlation matrix $\hat{C}_{T+1:T+h}$ over the next $h$ periods, $h \geq 2$, by the next period’s asset returns covariance matrix $\hat{\Sigma}_{T+1}$ and correlation matrix $\hat{C}_{T+1}$.

Indeed, from the previous sub-section, we have:

• $ \hat{\Sigma}_{T+1:T+h} = \frac{1}{h} \sum_{i=1}^{h} \hat{\Sigma}_{T+i} = \hat{\Sigma}_{T+1} $, $h \geq 2$
• $ \hat{C}_{T+1:T+h} = \frac{1}{h} \sum_{i=1}^{h} \hat{C}_{T+i} = \hat{C}_{T+1} $, $h \geq 2$

Rationale

The rationale behind the IEWMA covariance matrix forecasting model is twofold:

• Separate volatility forecasting from correlation matrix forecasting while using the same baseline forecasting model for internal consistency.

  This first idea is well known among practitioners, c.f. for example Menchero and Li¹⁰ which describes the usage of different EWMA half-lives for estimating volatilities and correlations¹¹.

• Use volatility-standardized asset returns instead of raw asset returns for correlation matrix forecasting.

  This second idea, detailled for example in Engle⁶, originates from the fact that conditional correlations between asset returns are equal to conditional covariances between standardized disturbances, c.f. the previous section.

  So, given an estimator for the (unobservable) standardized disturbances $\epsilon_{i,t} = \frac{r_{i,t}}{\sigma_{i,t}}$, $i=1..n$, $t=1..T$, it is possible to estimate the conditional correlations between asset returns.

  An example of such estimator is the volatility-standardized asset returns $\tilde{r}_{i,t} = \frac{r_{i,t}}{\hat{\sigma}_{i,t}}$, with the drawback that the quality of the correlation forecasts is then influenced by the quality of the volatility forecasts.

  And unfortunately, because it is well known that […] asset returns […] fat tails are typically reduced but not eliminated when returns are standardized by volatilities estimated from popular [volatility forecasting] models¹² and because the use of correlation as a measure of dependence can be misdealing in the case of (conditionally) non-Gaussian returns¹³, we should not expect any magic here…

How to choose the decay factors?

Due to its relationship with the vanilla EWMA volatility and covariance matrix forecasting models, there are two main procedures to choose the decay factors $\lambda_{vol}$ and $\lambda_{cor}$ of an IEWMA covariance matrix forecasting model:

• Using recommended values from the EWMA models literature (0.94, 0.97…).

  On this, Johansson et al.³ notes that empirical studies on real return data confirm that choosing a faster volatility half-life than correlation half-life yields better estimates⁶ and uses the following pairs of decay factors $\left(\lambda_{vol}, \lambda_{cor}\right)$ in their experimental setup:

  • Short term - $\left(0.870,0.933\right)$, $\left(0.933,0.967\right)$
  • Medium term - $\left(0.967,0.989\right)$, $\left(0.989,0.994\right)$, $\left(0.994,0.997\right)$
  • Long term - $\left(0.997,0.998\right)$, $\left(0.998,0.999\right)$

• Determining the optimal values w.r.t. the forecast horizon $h$, for example through the minimization of the root mean square error (RMSE) between the forecasted covariance matrix over the desired horizon and the observed covariance matrix over that horizon¹⁴.

  In practice, because there are two decay factors to choose, this can be done two ways:

  • Either consider the two decay factors as a two independent univariate parameters $\lambda_{vol} \in [0,1]$ and $\lambda_{cor} \in [0,1]$.

    This choice is justified by the original desire to separate volatility forecasting from correlation matrix forecasting.

  • Or consider the two decay factors as a single multivariate parameter $\left(\lambda_{vol}, \lambda_{cor}\right) \in [0,1]^2$.

    This choice is justified by the observed dependency of the correlation forecasts on the volatility-standardized asset returns.

Extensions of the iterated exponentially weighted moving average covariance matrix forecasting model

Asset-specific volatility decay factors

The IEWMA covariance matrix forecasting model uses univariate EWMA models in order to forecast asset volatilities, all these models sharing the same decay factor $\lambda_{vol}$.

Having an identical decay factor for all assets is parsimonious, but is somewhat at odds with the DCC-GARCH model of Engle⁶ which uses asset-specific univariate GARCH models - that is, each with its own asset-specific parameters - in order to forecast asset volatilities.

So, one natural extension of the IEWMA model is to allow asset-specific univariate EWMA models - each with its own asset-specific decay factor $\lambda_{i,vol}$, $i=1..n$ - in order to forecast asset volatilities.

Linear combination of IEWMA covariance matrix forecasting models

Another interesting covariance matrix forecasting model is introduced in Johansson et al.³ as the combined multiple iterated exponentially weighted moving average (CM-IEWMA) model, which consist in a time-varying linear combination of individual IEWMA models, each with its own pair of fixed decay factors.

As explained in Johansson et al.³:

The CM-IEWMA predictor is constructed from a modest number of IEWMA predictors, with different pairs of half-lives, which are combined using dynamically varying weights that are based on recent performance.

The rationale behind the CM-IEWMA model is that different pairs of half-lives may work better for different market conditions³, with short half-lives [typically performing] better in volatile markets [and] long half-lives [performing] better for calm markets where conditions are changing slowly³.

This behaviour is illustrated in Figure 1, taken from Johansson et al.³, which shows the evolution of the weights of a 5-IEWMA CM-IEWMA covariance matrix forecasting model applied to a universe of U.S. stocks.

Figure 1. Evolution of the weights of a 5-IEWMA CM-IEWMA covariance matrix forecasting model applied to a universe of U.S. stocks, 4th January 2010 - 30th December 2022. Source: Johansson et al.

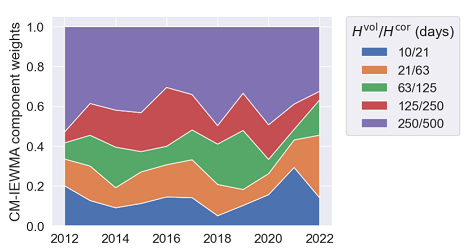
From Figure 1, it is visible that although substantial weight is put on the slower (longer halflife) IEWMAs most years³, the CM-IEWMA model still adapts the weights depending on market conditions³.

The interested reader is referenced to Johansson et al.³ for all the technicalities of the CM-IEWMA model, and in particular for the details about the computation of the dynamically varying weights of the individual IEWMA models through the resolution of a convex optimization problem¹⁵.

A last important remark to conclude this sub-section - the CM-IEWMA model is actually a special case of [a more general] dynamically weighted prediction [model]³, so that the same weighting logic can be applied to any combination of covariance matrix forecasting models.

Implementations

Implementation in Portfolio Optimizer

Portfolio Optimizer implements the IEWMA covariance and correlation matrix forecasting model through the endpoints /assets/covariance/matrix/forecast/iewma and /assets/correlation/matrix/forecast/iewma.

These endpoints support the 2 covariance proxies below:

• Squared (close-to-close) returns
• Demeaned squared (close-to-close) returns

These endpoints also allow:

• To use asset-specific univariate EWMA models in order to forecast asset volatilities
• To automatically determine the optimal value of their parameters (the decay factors $\lambda_{vol}$ and $\lambda_{cor}$) using a proprietary procedure.

To be noted that Portfolio Optimizer does not provide any implementation of the CM-IEWMA model¹⁶, but c.f. the next sub-section.

Implementation elsewhere

Johansson et al.³ kindly provides an open source Python implementation of:

• The IEWMA covariance matrix forecasting model
• The CM-IEWMA covariance matrix forecasting model
• The general “covariance matrix forecasting models” combination model

at https://github.com/cvxgrp/cov_pred_finance.

I definitely encourage anyone interested in the CM-IEMWA model to play with this code!

Example of usage - Covariance matrix forecasting at monthly level for a portfolio of various ETFs

As an example of usage, I propose to evaluate the empirical performances of the IEWMA covariance matrix forecating model within the framework of the previous blog bost, whose aim is to forecast monthly covariance and correlation matrices for a portfolio of 10 ETFs representative¹⁷ of misc. asset classes:

• U.S. stocks (SPY ETF)
• European stocks (EZU ETF)
• Japanese stocks (EWJ ETF)
• Emerging markets stocks (EEM ETF)
• U.S. REITs (VNQ ETF)
• International REITs (RWX ETF)
• U.S. 7-10 year Treasuries (IEF ETF)
• U.S. 20+ year Treasuries (TLT ETF)
• Commodities (DBC ETF)
• Gold (GLD ETF)

Results - Covariance matrix forecasting

Results over the period 31st January 2008 - 31st July 2023¹⁸ for covariance matrices are the following¹⁹:

Covariance matrix model	Covariance matrix MSE
SMA, window size of all the previous months (historical average model)	9.59 $10^{-6}$
SMA, window size of the previous year	9.08 $10^{-6}$
EWMA, optimal20 $\lambda$	6.52 $10^{-6}$
EWMA, $\lambda = 0.97$	6.37 $10^{-6}$
IEWMA, $\left(\lambda_{vol},\lambda_{cor}\right) = \left(0.97,0.99\right)$	6.35 $10^{-6}$
IEWMA, optimal20 $\lambda_{i,vol}$, $i=1..n$ and $\lambda_{cor}$	6.33 $10^{-6}$
IEWMA, optimal20 $\left(\lambda_{vol},\lambda_{cor}\right)$	6.16 $10^{-6}$
SMA, window size of the previous month (random walk model)	6.06 $10^{-6}$
EWMA, $\lambda = 0.94$	5.78 $10^{-6}$
IEWMA, $\left(\lambda_{vol},\lambda_{cor}\right) = \left(0.94,0.97\right)$	5.78 $10^{-6}$

Within this specific evaluation framework, the IEWMA covariance matrix forecasting model unfortunately does not seem to improve upon the previous models despite the added complexity.

It is also noteworthy that the IEWMA model with asset-specific univariate EWMA models for volatility (line #6) does not exhibit better performances than the vanilla IEWMA model (line #7) when using automatically determined parameters²¹.

Results - Correlation matrix forecasting

Results over the period 31st January 2008 - 31st July 2023¹⁸ for the correlation matrices associated to the covariance matrices of the previous sub-section are the following¹⁹:

Covariance matrix model	Correlation matrix MSE
SMA, window size of the previous month (random walk model)	8.19
SMA, window size of all the previous months (historical average model)	8.10
EWMA, $\lambda = 0.94$	7.67
SMA, window size of the previous year	6.50
EWMA, $\lambda = 0.97$	6.36
EWMA, optimal20 $\lambda$	5.87
IEWMA, $\left(\lambda_{vol},\lambda_{cor}\right) = \left(0.94,0.97\right)$	5.85
IEWMA, $\left(\lambda_{vol},\lambda_{cor}\right) = \left(0.97,0.99\right)$	5.85
IEWMA, optimal20 $\lambda_{i,vol}$, $i=1..n$ and $\lambda_{cor}$	5.72
IEWMA, optimal20 $\left(\lambda_{vol},\lambda_{cor}\right)$	5.70

This time, the IEWMA model - and especially the two IEWMA models using automatically determined parameters (lines #9-#10) - does exhibit slightly better performances than all the previous models.

Nevertheless, the improvement over the previously best-performing model (line #6 - the EWMA model with automatically determined parameter) is not that impressive…

So, the idea of removing the impact of volatility on asset returns in order to better estimate asset correlations seems to have some merits, but the EWMA volatility forecasting model might be insufficient to fully exploit this idea.

Also, here again, the performances of the IEWMA model with asset-specific univariate EWMA models for volatility are again strictly worse than the performances of the vanilla IEWMA model²¹.

Conclusion

One of the main characteristics of the IEWMA covariance matrix forecasting model of Johansson et al.³ is to forecast asset correlations using (EWMA-)volatility-standardized asset returns instead of raw asset returns, so that the impact of asset volatilities on their correlations is (tentatively) minimized.

Unfortunately, the empirical performances of that model in terms of correlation matrix forecasting are not that different from those of the EWMA model, which raises the question of whether improving the volatility-standardization might lead to better correlation forecasts.

This will be the subject of a future blog post in this series.

As usual, feel free to connect with me on LinkedIn or to follow me on Twitter.

–

1. ChatGPT-generated, as can be seen by the signature word “delve” :-) ! ↩

2. At the date of the initial publication of this blog post. ↩

3. See Kasper Johansson, Mehmet G. Ogut, Markus Pelger, Thomas Schmelzer and Stephen Boyd (2023), A Simple Method for Predicting Covariance Matrices of Financial Returns, Foundations and Trends in Econometrics: Vol. 12: No. 4, pp 324-407. ↩ ↩² ↩³ ↩⁴ ↩⁵ ↩⁶ ↩⁷ ↩⁸ ↩⁹ ↩¹⁰ ↩¹¹ ↩¹² ↩¹³ ↩¹⁴ ↩¹⁵ ↩¹⁶

4. See Valeriy Zakamulin, A Test of Covariance-Matrix Forecasting Methods, The Journal of Portfolio Management Spring 2015, 41 (3) 97-108. ↩ ↩²

5. See Patton, A.J., Sheppard, K. (2009). Evaluating Volatility and Correlation Forecasts. In: Mikosch, T., Kreiß, JP., Davis, R., Andersen, T. (eds) Handbook of Financial Time Series. Springer, Berlin, Heidelberg. ↩

6. See Engle, R. (2002). Dynamic Conditional Correlation. Journal of Business & Economic Statistics. 20(3): 339–350. ↩ ↩² ↩³ ↩⁴ ↩⁵ ↩⁶ ↩⁷ ↩⁸ ↩⁹ ↩¹⁰ ↩¹¹

7. That being said, I find that what Engle⁶ describes is closer to an iterated $n$-univariate GARCH volatility forecasting models/EWMA correlation matrix forecasting model than to the iterated EWMA forecasting model of Johansson et al.³… ↩

8. C.f. the associated blog posts here and there. ↩

9. See Gianluca De Nard, Robert F. Engle, Olivier Ledoit, Michael Wolf, Large dynamic covariance matrices: Enhancements based on intraday data, Journal of Banking & Finance, Volume 138, 2022, 106426. ↩

10. See Menchero, Jose and Peng Li. Correlation Shrinkage: Implications for Risk Forecasting, Journal of Investment Management (2020). ↩

11. Digging a little deeper, the old MAC1 and MAC2 Bloomberg multi-asset risk models were using an half-life of 26 weeks for estimating volatilities and an half-life of 52 weeks for estimating correlations. ↩

12. See Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Paul Labys, 2000, Exchange Rate Returns Standardized by Realized Volatility are (Nearly) Gaussian, Multinational Finance Journal 4, 159-179.. ↩

13. See Bahram Pesaran, M. Hashem Pesaran, Conditional volatility and correlations of weekly returns and the VaR analysis of 2008 stock market crash, Economic Modelling, Volume 27, Issue 6, 2010, Pages 1398-1416. ↩

14. See RiskMetrics. Technical Document, J.P.Morgan/Reuters, New York, 1996. Fourth Edition. ↩

15. The maximization of the average log-likelihood of the combined [covariance matrix] prediction over [a trailing number of periods]³. ↩

16. This is because my own tests did not highlight any strong improvement in terms of forecasting ability v.s. the IEWMA model when used with an optimal pair of decay factors. ↩

17. These ETFs are used in the Adaptative Asset Allocation strategy from ReSolve Asset Management, described in the paper Adaptive Asset Allocation: A Primer²². ↩

18. (Adjusted) daily prices have have been retrieved using Tiingo. ↩ ↩²

19. Using the outer product of asset returns - assuming a mean return of 0 - as covariance proxy, and using an expanding historical window of asset returns. ↩ ↩²

20. The optimal decay factors ($\lambda$, $\lambda_{vol}$, $\lambda_{cor}$) are computed at the end of every month using all the available asset returns history up to that point in time, as implemented in Portfolio Optimizer; thus, there is no look-ahead bias. ↩ ↩² ↩³ ↩⁴ ↩⁵ ↩⁶

21. The difference between the two models is probably just noise, which, at worst, implies that the added complexity of the IEWMA model with asset-specific univariate EWMA models is useless in practice. ↩ ↩²

22. See Butler, Adam and Philbrick, Mike and Gordillo, Rodrigo and Varadi, David, Adaptive Asset Allocation: A Primer. ↩